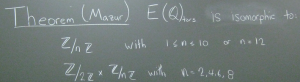
Image courtesy of Andrew Snowden under a Creative Commons license: BY.
Math 679 is a graduate level mathematics course whose purpose is to prove Mazur's theorem. Mazur's theorem is a well-known and important result, however it is not often taught in classroom settings. The course is divided into three parts: elliptic curves and abelian varieties, moduli of elliptic curves, and proof of Mazur’s theorem.
Schedule
Lecture 1: Overview
Part I: Elliptic curves and abelian varieties
Lectures 2, 3, 4: Elliptic curves and abelian varieties over fields
Lectures 5, 6, 7: Group schemes, over fields and DVRs, including Raynaud’s theorem
Lectures 8, 9: Abelian varieties in mixed characteristic, including Néron models
Lecture 10: Jacobians
Lecture 11: Criterion for rank 0 (Theorem B from Lecture 1)
Part II: Moduli of elliptic curves
Lectures 12, 13, 14: Modular curves
Lecture 15, 16: Modular forms and the Hecke algebra
Lecture 17: The Eichler–Shimura theorem
Lectures 18, 19: Criterion for non-existence of torsion (Theorem A from Lecture 1)
Part III: Proof of Mazur’s theorem
Lecture 20: The Eisenstein ideal and Eisenstein quotient of J0(N)
Lectures 21, 22: The special fiber at N of J0(N)
Lecture 23: Ogg’s theorem on the order of [∞]−[0] in J0(N)
Lectures 24, 25, 26, 27: TBA
About the Creators

Andrew Snowden
Andrew Snowden is an assistant professor of mathematics at the University of Michigan.
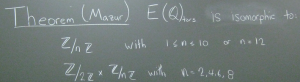
Image courtesy of Andrew Snowden under a Creative Commons license: BY.
Jump to:
| Document Title | Creator | Downloads | License |
|---|---|---|---|
|
Lecture 01: Exercise 1 |
Andrew Snowden
|
| Document Title | Creator | Downloads | License |
|---|---|---|---|
|
Lecture 01: Overview |
Andrew Snowden
|
||
|
Lecture 02: Elliptic curves |
Andrew Snowden
|
||
|
Lecture 03: Abelian varieties (analytic theory) |
Andrew Snowden
|
||
|
Lecture 04: Abelian varieties (algebraic theory) |
Andrew Snowden
|
||
|
Lecture 05: Group schemes 1 |
Andrew Snowden
|
||
|
Lecture 06: Group schemes 2 |
Andrew Snowden
|
||
|
Lecture 07: Group schemes 3 |
Andrew Snowden
|
||
|
Lecture 08: Elliptic curves over DVRs |
Andrew Snowden
|
||
|
Lecture 09: Néron models |
Andrew Snowden
|
||
|
Lecture 10: Jacobians |
Andrew Snowden
|
||
|
Lecture 11: Criterion for rank 0 |
Andrew Snowden
|
| Document Title | Creator | Downloads | License |
|---|---|---|---|
|
Lecture 01: Overview |
Andrew Snowden
|
||
|
Lecture 02: Elliptic curves |
Andrew Snowden
|
||
|
Lecture 03: Abelian varieties (analytic theory) |
Andrew Snowden
|
||
|
Lecture 04: Abelian varieties (algebraic theory) |
Andrew Snowden
|
||
|
Lecture 05: Group schemes 1 |
Andrew Snowden
|
||
|
Lecture 06: Group schemes 2 |
Andrew Snowden
|
||
|
Lecture 07: Raynaud’s theorem |
Andrew Snowden
|
||
|
Lecture 08: Elliptic curves over DVRs |
Andrew Snowden
|
||
|
Lecture 09: Néron models |
Andrew Snowden
|
||
|
Lecture 10: Jacobians |
Andrew Snowden
|
||
|
Lecture 11: Criterion for rank 0 |
Andrew Snowden
|
||
|
Lecture 12: Modular curves over C |
Andrew Snowden
|
||
|
Lecture 13: Modular forms |
Andrew Snowden
|
||
|
Lecture 14: Lecture 14: Modular curves over Q |
Andrew Snowden
|
||
|
Lecture 15: Modular curves over Z |
Andrew Snowden
|
||
|
Lecture 16: Structure of the Hecke algebra |
Andrew Snowden
|
||
|
Lecture 17: Eichler–Shimura |
Andrew Snowden
|
||
|
Lecture 18: Criterion for non-existence of torsion points |
Andrew Snowden
|
||
|
Lecture 19: J0(N) mod N |
Andrew Snowden
|
||
|
Lecture 20: Proof of Mazur’s theorem (part 1) |
Andrew Snowden
|
||
|
Lecture 21: Proof of Mazur’s theorem (part 2) |
Andrew Snowden
|
||
|
Lecture 22: 13 torsion |
Andrew Snowden
|
||
|
Lecture 23: Finishing up |
Andrew Snowden
|
| Document Title | Creator | Downloads | License |
|---|---|---|---|
|
References |
Andrew Snowden
|
| Document Title | Creator | Downloads | License |
|---|---|---|---|
|
Plan |
Andrew Snowden
|
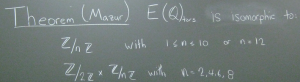
Image courtesy of Andrew Snowden under a Creative Commons license: BY.
Jump to:
| Document Title | Creator | Downloads | License |
|---|---|---|---|
|
Lecture 01: Overview |
Andrew Snowden
|
||
|
Lecture 02: Elliptic curves |
Andrew Snowden
|
||
|
Lecture 02: Elliptic curves |
Andrew Snowden
|
||
|
Lecture 03: Abelian varieties (analytic theory) |
Andrew Snowden
|
||
|
Lecture 03: Abelian varieties (analytic theory) |
Andrew Snowden
|
||
|
Lecture 04: Abelian varieties (algebraic theory) |
Andrew Snowden
|
||
|
Lecture 05: Group schemes 1 |
Andrew Snowden
|
||
|
Lecture 05: Group schemes 1 |
Andrew Snowden
|
||
|
Lecture 06: Group schemes 2 |
Andrew Snowden
|
||
|
Lecture 06: Group schemes 2 |
Andrew Snowden
|
||
|
Lecture 07: Raynaud’s theorem |
Andrew Snowden
|
||
|
Lecture 08: Elliptic curves over DVRs |
Andrew Snowden
|
||
|
Lecture 08: Elliptic curves over DVRs |
Andrew Snowden
|
||
|
Lecture 09: Néron models |
Andrew Snowden
|
||
|
Lecture 10: Jacobians |
Andrew Snowden
|
||
|
Lecture 10: Jacobians |
Andrew Snowden
|
||
|
Lecture 11: Criterion for rank 0 |
Andrew Snowden
|
||
|
Lecture 11: Criterion for rank 0 |
Andrew Snowden
|
| Document Title | Creator | Downloads | License |
|---|---|---|---|
|
Lecture 12: Modular curves over C |
Andrew Snowden
|
||
|
Lecture 13: Modular forms |
Andrew Snowden
|
||
|
Lecture 14: Lecture 14: Modular curves over Q |
Andrew Snowden
|
||
|
Lecture 15: Modular curves over Z |
Andrew Snowden
|
||
|
Lecture 16: Structure of the Hecke algebra |
Andrew Snowden
|
||
|
Lecture 17: Eichler–Shimura |
Andrew Snowden
|
||
|
Lecture 18: Criterion for non-existence of torsion points |
Andrew Snowden
|
||
|
Lecture 19: J0(N) mod N |
Andrew Snowden
|
| Document Title | Creator | Downloads | License |
|---|---|---|---|
|
Lecture 20: Proof of Mazur’s theorem (part 1) |
Andrew Snowden
|
||
|
Lecture 21: Proof of Mazur’s theorem (part 2) |
Andrew Snowden
|
||
|
Lecture 22: 13 torsion |
Andrew Snowden
|
||
|
Lecture 23: Finishing up |
Andrew Snowden
|

